Página inicial > Tecnologias de Comunicação Aplicadas à Educação Matemática > Aula 2

Catalão , Abril 2009” é uma oficina que tem como propósito discutir e avaliar as possibilidades pedagógicas dos softwares de geometria dinâmica, quando se pensa no ensino da geometria escolar.

Nessa oficina o autor utiliza como exemplo o software “Régua e Compasso” que é uma ferramenta que possibilita situações de aprendizagem que se caracterizam como: experimentar, interpretar, visualizar, induzir, conjeturar, abstrair, generalizar e até demonstrar. Ele ensina como construir algumas figuras geométricas, e como trabalhar com algumas das inúmeras ferramentas que esse software dispõe. Faz algumas demonstrações utilizando o software como, por exemplo, o clássico Teorema de Pitágoras. Argumenta como é mais fácil entender os conceitos da geometria através desse software, pois a partir de uma coleção de desenhos em movimento podemos evidenciar o propósito de organizar o conhecimento na forma de teoria dedutiva – axiomas, definições, teoremas e demonstrações. Isto porque, nele temos os fatos declarados nos passos da construção que encerram regularidades não explicitadas e que se tornam, portanto, passíveis de explicação.

O autor ainda argumenta que: “Os ambientes de geometria dinâmica permitem um novo tratamento para os enunciados clássicos da geometria: teoremas passam a ser vistos não como propriedades estáticas, mas como casos especiais de certa classe de desenhos em movimento. O mundo que nos rodeia está repleto de situações em que a geometria se faz presente. E mais, são situações em que formas geométricas se apresentam em movimento. A modelação destas “formas em movimento”, quer sejam de caráter prático ou lúdico, pode propiciar o desenvolvimento de conceitos e relações geométricas e, assim sendo, apresenta-se como uma atividade que pode ser interessante para os alunos que estão se iniciando no estudo da geometria.”.

Enfim a oficina nos ensina a trabalhar com a Geometria em sala de aula de um ponto de vista diferente, mais dinâmico, e às vezes, mais atrativo para os alunos, pois trabalha com a realidade deles, e principalmente de uma forma mais lúdica e com ferramentas (o computador) que eles já estão acostumados a trabalhar.

2.          Conheça o site Portal dos Professores de Matemática. Entre no link sobre Geometria Dinâmica. Faça uma resenha desse link para sua página.

O Portal Do Professores de Matemática e um site dedicado ao ensino da matemática que possui vários conteúdos interessantes de diversas series, com dicas de como aplicá-los em sala de aula. O site possui vários links de softwares e jogos associados a esses conteúdos, para que o professor possa diversifica suas estratégias de ensino. Alem de trazer informação de vários cursos, concursos, vídeos e etc. Na parte de Geometria Dinâmica o site traz algumas sugestões de softwares para serem utilizados em sala de aula, para facilitar o ensino de Geometria, uma matéria as vezes muito abstrata para os alunos. Traz também um tutorial de como utilizar o software CAR e sugestões de conteúdos que podem ser trabalhos através desses programas. E um site muito interessante para nos professores, que ajuda muito na nossa busca por uma aula mais atrativa para nossos alunos.

3. Baixe e teste o CAR e o Geogebra em seu computador. Resenhe os programas em sua página.

GeoGebra é um programa livre de geometria dinâmica criado por Markus Hohenwarter para ser utilizado em ambiente de sala de aula. Seu criador, Markus Hohenwarter, iniciou o projeto em 2001 na University of Salzburg e tem continuado o desenvolvimento na Florida Atlantic University. O GeoGebra é escrito em Java e assim está disponível em múltiplas plataformas.

Por um lado, o GeoGebra é um programa de geometria dinâmica. Você pode realizar construções utilizando pontos, vetores, segmentos, retas, seções cônicas bem como funções e alterar todos esses objetos dinamicamente após a construção estar finalizada. Por outro lado, podem ser incluídas equações e coordenadas diretamente. Assim, o GeoGebra é capaz de lidar com variáveis para números, vetores e pontos, derivar e integrar funções e ainda oferece comandos para encontrar raízes e pontos extremos de uma função. Deste modo, o programa reúne as ferramentas tradicionais de geometria, com outras mais adequadas à álgebra e ao cálculo. Assim tem a vantagem didática de apresentar, ao mesmo tempo, duas representações diferentes de um mesmo objeto que interagem entre si: sua representação geométrica e sua representação algébrica.

Diferentemente do que ocorre com a régua e o compasso tradicionais, as construções feitas com o “Régua e Compasso” são dinâmicas e interativas, o que faz do programa um excelente laboratório de aprendizagem da geometria. O aluno (ou o professor) pode testar suas conjecturas através de exemplos e contra-exemplos que ele pode facilmente gerar. Uma vez feita a construção, pontos, retas e círculos podem ser deslocados na tela mantendo-se as relações geométricas (pertinência, paralelismo, etc.) previamente estabelecidas, permitindo assim que o aluno (ou o professor), ao invés de gastar o seu tempo com detalhes de construção repetitivos, se concentre na associação existente entre os objetos.

4. Construa, usando o CAR e o Geogebra, um polígono regular com n lados, sendo n o último algarismo do número de sua matrícula, caso este algarismo seja entre 5 e 9. Se o último algarismo for entre 0 a 4, construa um polígono de n+10 lados.

Geogebra



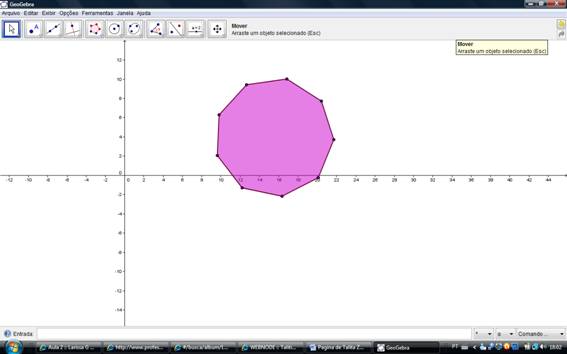
CAR

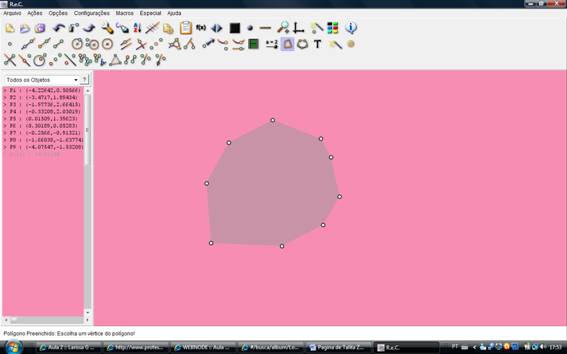
5.          Escreva um texto intitulado Trabalhando com geometria dinâmica na escola e coloque em sua página.

Um dos objetivos da geometria é conduzir os alunos a terem uma leitura geométrica dos desenhos. O computador pode contribuir para que o aluno tenha uma leitura e exploração dos desenhos em termos geométricos. Nos dias atuais, com o uso da informática, cresce o número de programas usados para o ensino e aprendizagem da matemática. Disciplinas como Cálculo, Álgebra Linear, Estatística e algumas disciplinas da Física, também fazem uso de algum software em seu processo de ensino. Já não é de hoje que software é usado em escolas e faculdades. A idéia é dar um acesso com possibilidades de cálculo e representações do computador ao conjunto de desenhos representando a mesma figura. Esse acesso é através da geometria dinâmica. A característica dinâmica aparece pela possibilidade de se passar de um desenho a outro pelo deslocamento quase contínuo dos objetos com "graus de liberdade".

A geometria dinâmica não é a geometria euclidiana ou uma das geometrias não-euclidianas. Os diversos softwares de geometria dinâmica implementam modelos de geometria diferentes. Cada implementação da geometria dinâmica, além de ter as características da geometria que servem de modelo, tem também propriedades específicas. De uma certa forma, ela constitui uma extensão dessas geometrias.

Existem vários softwares de Geometria Dinâmica, alguns deles são: O Graphmática, O Geogebra, o K3Dsurf e o Poly que respectivamente auxiliam nas aulas de Funções e Cálculo; Geometria (Plana e Analítica), Cálculo com duas variáveis reais e Geometria Espacial.

Esses softwares são uma boa maneira de atrair a atenção dos alunos para a Geometria, uma matéria muitas vezes esquecida pelos professores, por sua complexidade e difícil demonstração, e também de diversificar as aulas de matemática, abrindo para os professores um leque de novas possibilidades e idéias.

Contatos